This is part of a series on little things I learned while doing the problems from Advent of Code 2023. It won’t fully explain any problems or solutions from AOC. You can find all my solutions on Github.

Day 18 involves taking an irregular rectilinear shape and finding the area of it. Specifically, taking a list of directions (right 6, down 5, etc.) and turning it into an enclosed shape:

#######
#.....#
###...#
..#...#
..#...#
###.###
#...#..
##..###
.#....#
.######

then finding the number of squares enclosed, including those on the boundary.

For directions with small length n, this is easy to “brute-force” so to speak, with methods like like a flood fill algorithm, or ray-casting on each row to count the interior points.

But, in part 2 of the problem, the n on each direction becomes very large — larger than is reasonable to use any algorithm that is \(O(n)\). It turns out there is an analytical solution one can use instead, which derives the polygon area from the coordinates of its vertices.

Shoelace formula

The shoelace formula gives the area of a simple polygon (read: a single closed shape with no intersecting edges)¹:

The geometric intuition for why this works is that each pair of \((x, y)\) coordinates for \(i\) and \(i+1\) form a trapezoid with the \(x\)-axis. This trapezoid has area

where \(a\), \(b\) are the lengths of the parallel sides, as usual.

These trapezoid areas add to the polygon area when \(x_i > x_{i+1}\) (i.e., traveling from \(P_i \rightarrow P_{i+1} \) is to the left), and subtract from the area when traveling to the right², as illustrated via Wikipedia, below:

The areas below the polygon are subtracted from the larger trapezoids formed by the points on the top of the shape.

Pick’s theorem

The shoelace formula gives us to get the area with the points formed by the directions in the Advent of Code problem, but this is different than what is asked for — we need the number of squares enclosed by the shape, including the boundary.

The crux of the difference between the area of the shape and the number of points in it is that a line of length 1 from \((0, 0)\) to \((0, 1)\) contains 2 points. So take a simple square with side length 1, would look like this in the Advent of Code problem:

....
.##.
.##.
....

but like this when the # coordinates are translated to points on the hypothetical cartesian plane:

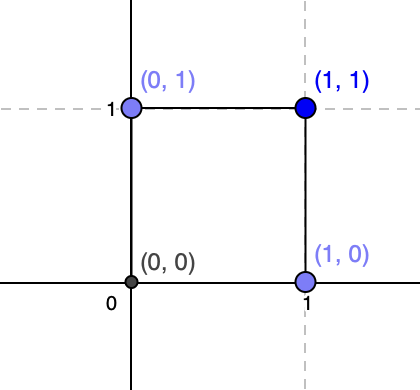
The points form a shape with 4 boundary points, but area 1.

It turns out there’s another formula relating a polygon’s area \(A\) to the number of boundary points \(b\) and interior points \(i\), called Pick’s theorem:

In AoC day 18, we can calculate \(A\) (using the Shoelace algorithm) and trivially compute \(b\)³, and the answer is the total number of points touched or enclosed by the path, \(b + i\):

My solution to the Advent of Code problem, written in Rust, is available here (link highlights the application of Shoelace and Pick’s theorem).